Within the lighting, the inverse square law is a term frequently heard. Despite seeming like a complex mathematical mind boggle, it is in fact a simple method to determine what happens when a subject moves father away from a light source.
The inverse square law represents how the intensity of a light reduces, when traveling away from its source. The reduction in brightness, is known as fall off. Fall off of light is not linear, meaning if you move the subject twice the distance from the light source, the intensity drops by a quarter and not half.
This process is achieved through a simple calculation: 1 divided by the distance squared.
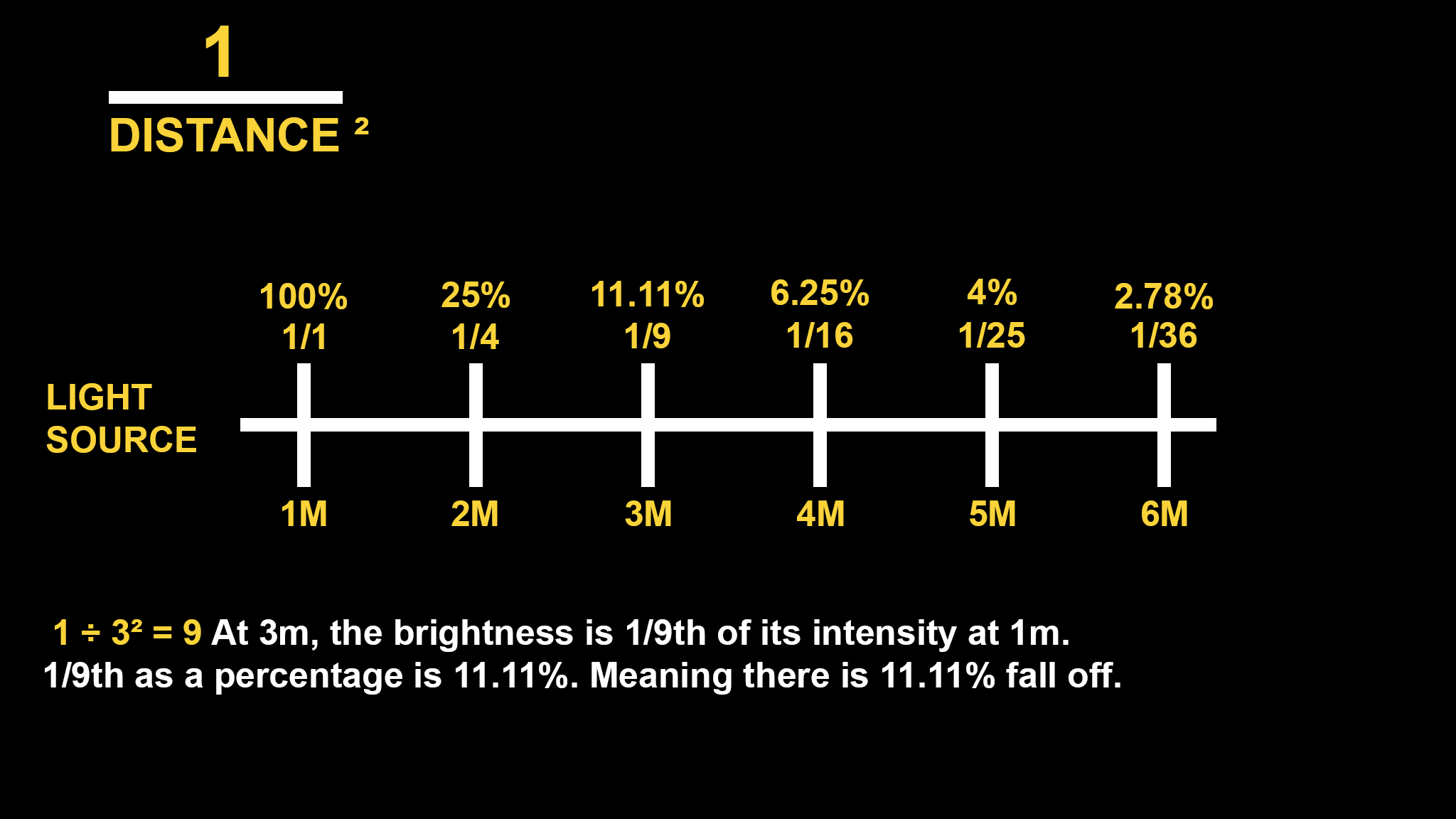
1 divided by 2 squared = 4. At 2m, the brightness is 1/4th of its intensity at 1m. ¼ as a percentage is 25%. Meaning there is 25% fall off.
1 divided by 4 squared = 16. At 4m, the brightness is 1/16th of its intensity at 1m. 1/6th as a percentage is 6.25%. Meaning there is 6.25% fall off.

At 2m, a 25% fall off creates a stronger contrast. The light is falling off before reaching the opposite side of the face.

At 4m, a 6.25% fall off creates a more even spread of light across the face. This is because the light has already travelled a fair distance from the source, before reaching the subjects face. From 2m to 4m, you would need to add two stops of light on the second subject for correct exposure.

If the first subject was at 3m and the second was at 4m, there wouldn’t be as greater fall off between, therefore you would be able to expose them both correctly in one reading. If you have multiple people at different distances, move the light further away for a less drastic fall off.
The same applies in terms of how you want the background to be lit. If the light is close to the subject, it will fall off drastically before reaching the background. If the light is father away from the subject, it will travel a greater distance and therefore have a decreased fall off.
How does this apply when looking at stops? -
Every time you double the distance from your subject to the light, the brightness increases or decreases by 75%, which is equivalent to two stops.
Doubling the distance of the light source = Losing two stops of light.
For example, the subject at 2m reads F16 on a light meter. The subject at 4m is under exposed by 2 stops, because the distance has doubled. At 4m you would need open up to F8 to correctly expose
Alternatively, at 4m you desire to shoot F2.8 but the light meter says F8. You would need to move the light double the distance away from the subject.
Aperture stops: F1.4, F2, F2.8, F4, F5.6, F8, F11, F16, F22, F32